Introduction
The aim of this article is to reveal the real nature of a cryptographic primitive called a Cryptographic Hash Function. Since the topic itself is quite mathematical, rigorous proofs will be omitted intentionally for the sake of simplicity. Therefore, expect less complex, but comprehensive models.
Functions
In the mathematical sense, a function is a mapping from one set (domain) to another set (codomain), where a set is just a bunch of unique elements grouped together. An intuitive way to think about the word “mapping” is that for each element in the domain, there is (not always) a corresponding element in the codomain. The way we denote sets is by assigning a capital letter to each of them. From a bird’s eye view, a function is a rule that allows us to associate elements from one set (domain) to another (codomain). An element in the domain we call a preimage and the corresponding element in the codomain we call an image.
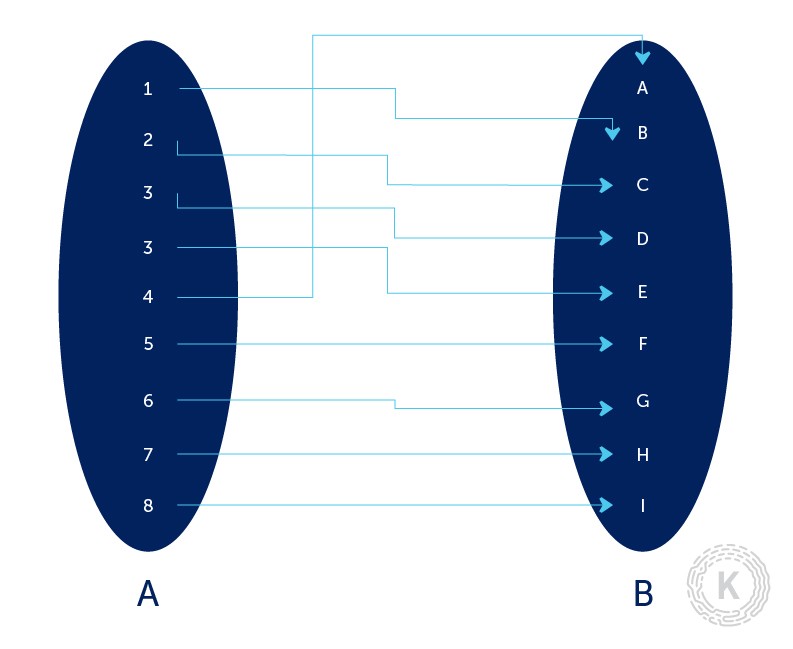
Keep in mind that a single element from the domain can map to only one distinct element in the codomain. If that property is not satisfied, what we have is not a real mathematical function. On the other hand, you can have multiple elements in the domain mapping to the same element in the codomain – that is perfectly fine and occurs regularly.
In some cases, as mentioned above, not every element from the domain has a corresponding element in the codomain. In that case, we can say that the function is not defined for a particular value from the domain. For example, the following function is defined for every integer x that is different from 0 since division by zero is an undefined operation in mathematics. In other words, for each element in set A (except 0) there is a corresponding element in the set B.
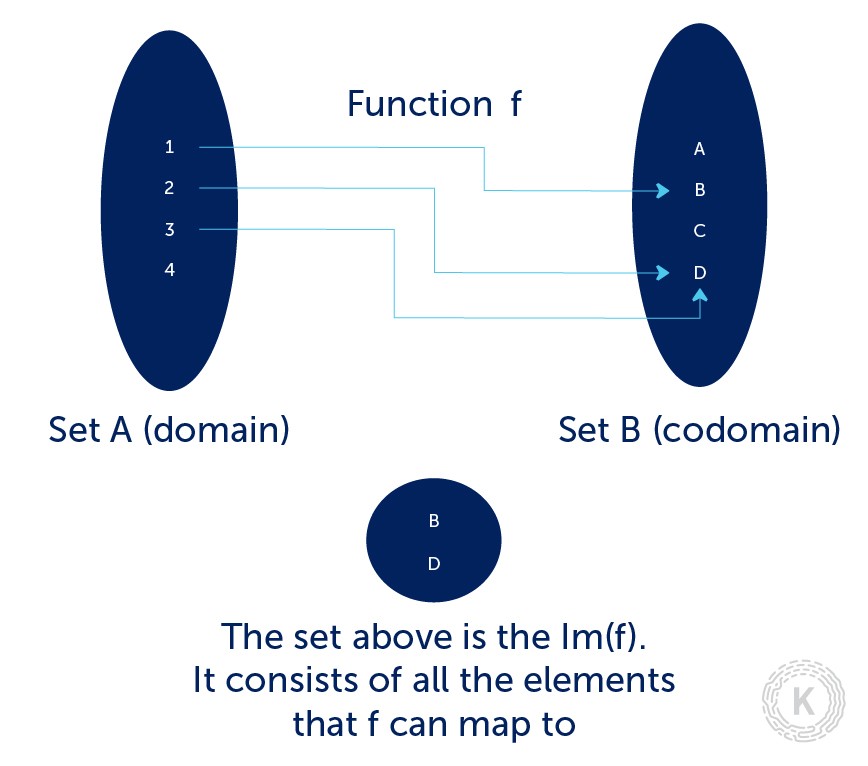
When working with such functions, we can use the notation which we read as the image of function . The image of function is the set of all elements that the function can map to. In other words, the image of function is a subset of the codomain:
One-way Functions
One-way functions play an integral role in cryptography. A simple mathematical definition would be:
“A one-way function is a rule/mapping from set A to set B where for each , is “easy” to compute but for “all” elements , it is “computationally infeasible” to find any such that .”
The reason we place words such as “easy” in quotes is that we still don’t know what they mean in the mathematical sense. Proofs and assumptions are two completely different things. And by saying “computationally infeasible” we are rather assuming than prooving.
Hash Functions
In this article, whenever we mention hash functions, we should always think about the cryptographic hash functions. Those functions that provide us an information security service (ISS for short) of some sort. In our case, cryptographic hash functions can relate to data integrity ISS or message authentication ISS.
The main hash function properties are inherent to both conventional hash functions that are used in a non-cryptographic manner and the cryptographic hash functions. These main properties are that each hash function should compress its input, in other words, we map an arbitrary size input to an output of a fixed size and they should not require a significant amount of computation.
More precisely, a hash function maps bitstrings of arbitrary finite length to strings of fixed length. If we have a larger set (domain A) of inputs of size t and a shorter set of outputs (codomain B) of size n, we can conclude that by definition, since t > n ( in other words we map a larger set onto a smaller set), we can conclude that collisions are unavoidable. Therefore, theoretically, we can always find two inputs that map to the same output.
The basic idea of cryptographic hash functions is that a hash-value serves as a compact representative image
Hash functions, generally, can be split into two main categories. Keyed hash functions (those that require an additional key to compute the hash of an element) and unkeyed hash functions (those that require only the element itself). From now on, we shall work only with unkeyed hash functions since the Blockchain Technology utilizes them heavily.
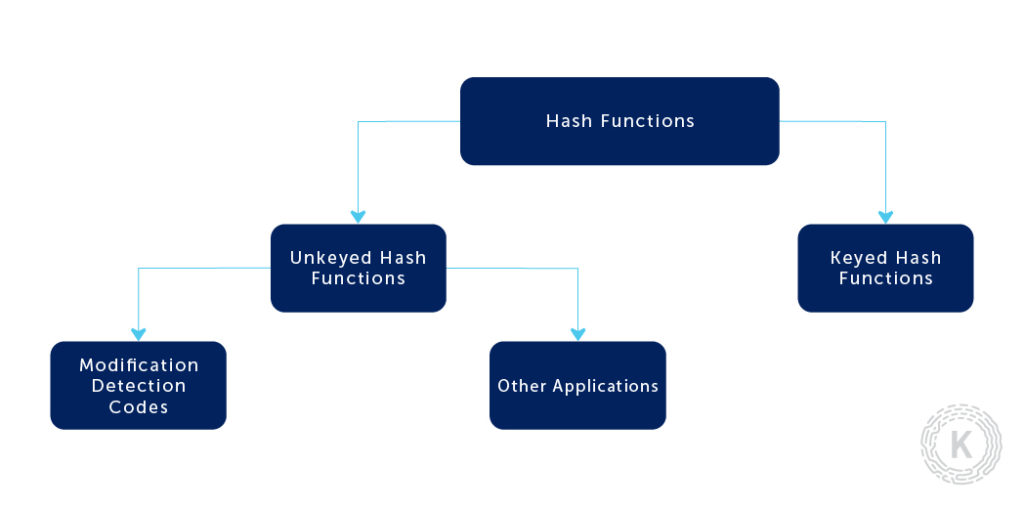
More specifically, we are going to talk about Modification Detection Codes (MDC). We can further split those into Collision-resistant Hash Functions (CRHF) and One-way Hash Functions (OWHF). There is a slight difference between the properties of the above-stated types. We define a hash function h with inputs x1 and x2 and corresponding outputs y1 and y2.
Preimage Resistance
It is computationally infeasible to find any input which hashes to a particular output, in other words, to find any preimage x such that h(x) = y when given any y for which a corresponding input is not known.
2nd Preimage Resistance
It is computationally infeasible to find any second input which has the same output as any specified input. For example, given x1, to find a 2nd-preimage x2 = x1 such that h(x1) = h(x2).
Collision-Resistance
It is computationally infeasible to find any two distinct inputs x1, x2 for which h(x1) = h(x2). (Note that here there is a free choice of both inputs.)
After defining the main properties besides compression of input and ease of computation, we shall specify which of these come in handy when talking about OWHF and CRHF.
A one-way hash function (OWHF) is a hash function with the additional properties of preimage resistance and 2nd-preimage resistance. That implies that one-time hash functions might be useful when you are certain that the adversary will have a particular input (preimage) and its corresponding output (image). To attack an OWHF, the adversary, given an image y, would need to find a preimage x such that y = h(x); or given one such pair (x1, h(x)), find a second preimage x2 such that h(x) = h(x).
A collision-resistant hash function (CRHF) is a hash function with the additional properties of 2nd-preimage resistance and collision resistance. To attack a CRHF, the attacker would need to find any two inputs x1, x2 such that h(x1) = h(x2).
Now that we have defined some of the cryptographic hash function types, you may realize that in order to use them efficiently, we need to understand the problem at hand and to put ourselves in the shoes of the adversary. Furthermore, there is a cost associated with specific properties. For example, to create a collision-resistant hash function, it usually needs to be twice the bit length of a one-way hash function.
In reality, we should be using a CRHF if an untrusted party has the ability to choose the inputs of the hash function (remember that one-way hash functions are not protected against chose plaintext attack or in other words finding two inputs that map to the same output). Otherwise, if the adversary is restricted, OWHF should be sufficient enough, including the case where there is only a single party involved (e.g., a store-and-retrieve application).
MDC + Asymmetric signature
In this case, the MDC will be used for an asymmetric signature where the plaintext that needs to be signed is hashed using a hash function h and then signed with a specific signing algorithm S. Here, we will need both preimage and 2nd preimage resistance. In a situation where the signed information (the preimage x1) and its hash (the image y) are public, and the hash function used – h is also publicly known, it should not be possible to find a preimage x2 that maps to the same image – h(x2) = y. That clarifies why we need a 2nd preimage resistance but does not explain at all why we need a preimage resistance. In a situation where the signed information, itself, is confidential, we should not be able to derive the preimage from the hash if we were to get ahold of the image.
Another important thing to consider is that if the adversary is able to choose the messages that are signed (chosen-plaintext attack), the hash function should also have the collision-resistance property.
MDC + symmetric encryption
In the case where both confidentiality and integrity are required, what we can do is use an MDC (h) to provide integrity check. We compute the image of the message h(message) = y, append it to the original message (message || y) and encipher it with a symmetric cipher. In that particular case, we won’t be needing preimage resistance, 2nd preimage resistance or collision-resistance. The idea is that the encryption protects the appended hash and that it be infeasible for an attacker without the encryption key to alter the message without disrupting the correspondence between the decrypted plaintext and the recovered MDC. Therefore the properties that the MDC must have can be significantly reduced. The only condition for the above statement is that it should not be feasible for an attacker to manipulate or create new ciphertext blocks so as to produce a new ciphertext which upon decryption will yield a message and its corresponding MDC (because that would be a forgery).
Hash for a one-way password file
In the case where you need to protect a password or another secret that is used for authentication purposes, standard practice would be to hash that secret/password and to keep the hash stored somewhere (usually on a server). In order to authenticate a counterparty, we can simply hash the secret/password he provides and compare to the hash that is already stored (we assume that the adversary won’t have write permissions to compromise the integrity of the stored image). In that case, in choosing an MDC that would do us a good job, we need to consider that 2nd preimage resistance and collision-resistance won’t be of much use since both of those attacks would require that the adversary has knowledge of the secret. Therefore, we can conclude that we only need preimage resistance.
Summary
Honestly, we could be talking all day long about hash functions. What is important is that a function is a mapping/a rule to associate elements from one set (domain) to another set (codomain) and in particular, hash functions are functions that map an element from an arbitrary size finite set to an always smaller (compression reasons) fixed size finite set. The two main properties of a hash function are the compression and the ease of computation property. We also need to remember that in the most generic sense, hash functions can be divided into keyed hash functions (their outputs rely on an additional factor) and unkeyed hash functions (the output is based only on the input). Furthermore, we can divide unkeyed hash functions into MDCs (Modification Detection Codes) and others. Specifically, MDCs can be further divided into CRHF (Collision-resistant hash functions and OWHF (One-way hash functions). And to conclude, both of these types require a subset of the following three properties – preimage resistance (having an output you cannot find an input that produces that output), 2nd preimage resistance (having an input and output pair you cannot find another input that produces the same output, also called weak-collision resistance) and collision resistance (finding two inputs that produce the same output, also called strong collision resistance).

